Una attività di matematica, con ragazzi APC
Minusio 15 marzo 2017
L’attività seguente è una realizzazione concreta di un PdP (o progetto pedagogico) che ha teso ad arricchire ed accelerare il programma di matematica di quarta classe elementare.
I tre problemi (più un quarto) che seguono, sono una variazione di una medesima situazione che da un punto di vista logico e matematico implica:
- La proiezione e il dispiegamento dei volumi
- Le proprietà del cubo
- Il calcolo additivo
- Il calcolo moltiplicativo
- Le potenze
- Calcolo esponenziale
- Le espressioni aritmetiche
- l’algebra
- Nomenclatura dei numeri
Da un punto di vista piu esecutivo: concentrazione, algoritmo della moltiplicazione scritta, incolonnamento, bella scrittura, perseveranza, ordine, programmazione delle tappe.
I tre problemi hanno una funzione introduttiva al calcolo algebrico, realizzato poi nel quarto problema.
Qui di seguito vediamo svolgimento dell’attività svolta in quattro unità didattiche, comprensiva della redazione in bella copia del percorso e dei risultati ottenuti.
Poi di seguito (seconda parte) altri ampliamenti.
Riassunto succinto.
Problema 1
Piero con i cubetti ha costruito un cubo più grande. Il lato del cubo ha 3 cubetti . Vedi disegno seguente.
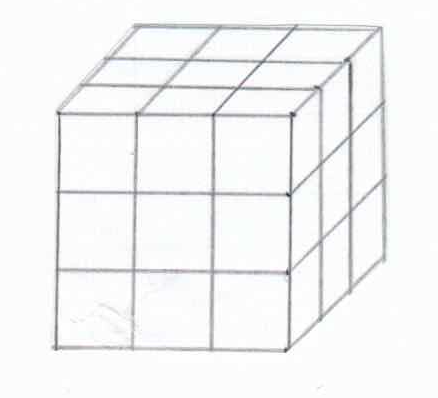
Domanda.
Quanti cubetti ha usato per costruire il cubo?
3 x 3 x 3 = 27
Poi Piero pittura il cubo di verde. Infine lo distrugge.
Domande
- Quanti cubetti non sono pitturati?
- Quanti cubetti hanno 1 faccia verde?
- Quanti cubetti hanno 2 facce verdi?
- Quanti cubetti hanno 3 facce verdi?
Risposte
- 1 cubetto
- 6 cubetti
- 12 cubetti
- 8 cubetti
Problema 2
Poi Piero con i cubetti ha costruito un cubo più grande. Il lato del cubo ha 4 cubetti . Vedi disegno seguente.
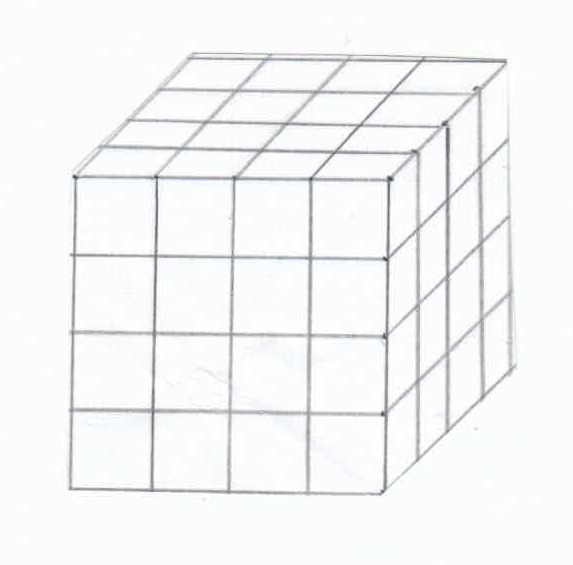
Quanti cubetti sono?
4 x 4 x 4 = 64 cubetti
Li pittura di rosso smonta il tutto.
Quanti restano bianchi? 4 + 4 = 8
Quanti hanno una faccia rossa? 24
Quanti hanno 2 facce rosse? 64 – (8 + 8 + 24) = 24
Quanti hanno 3 facce rosse? 8
Problema 3
Infine, Piero con i cubetti ha costruito un cubo più grande. Il lato del cubo ha 5 cubetti . Vedi disegno seguente.
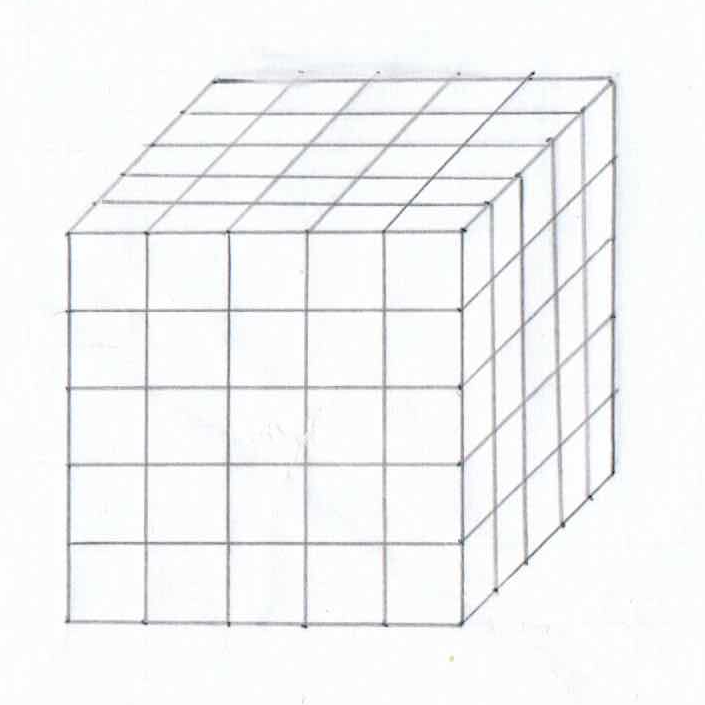
Quanti cubetti? 5 x 5 x 5 = 125
0 facce pitturate? (3 x3) x 3= 27
1 faccia pitturata? (3 x 3) x 6= 54
2 facce pitturate? 36 = 3 x 12
3 facce pitturate? 8
Problema 4
Piero costruisce altri cubi, di N (numero sconosciuto) cubetti.
Scopri le regole e scrivi la formula che va bene per tutti i cubi.
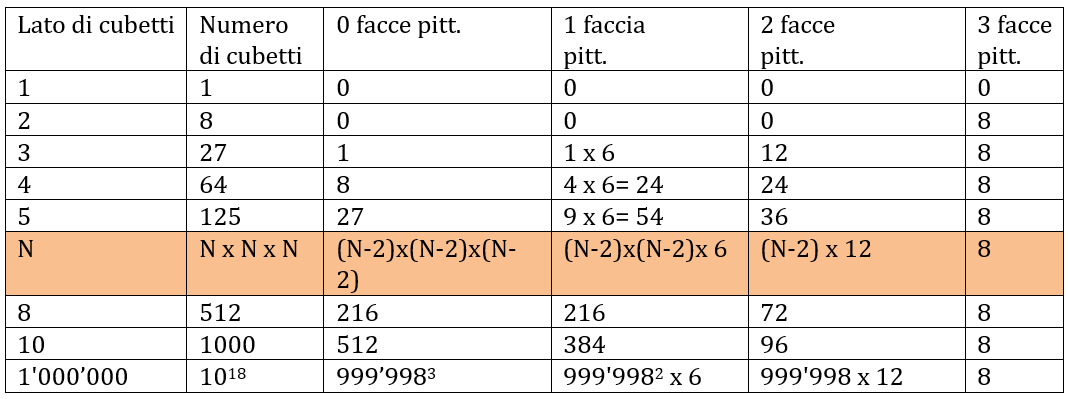
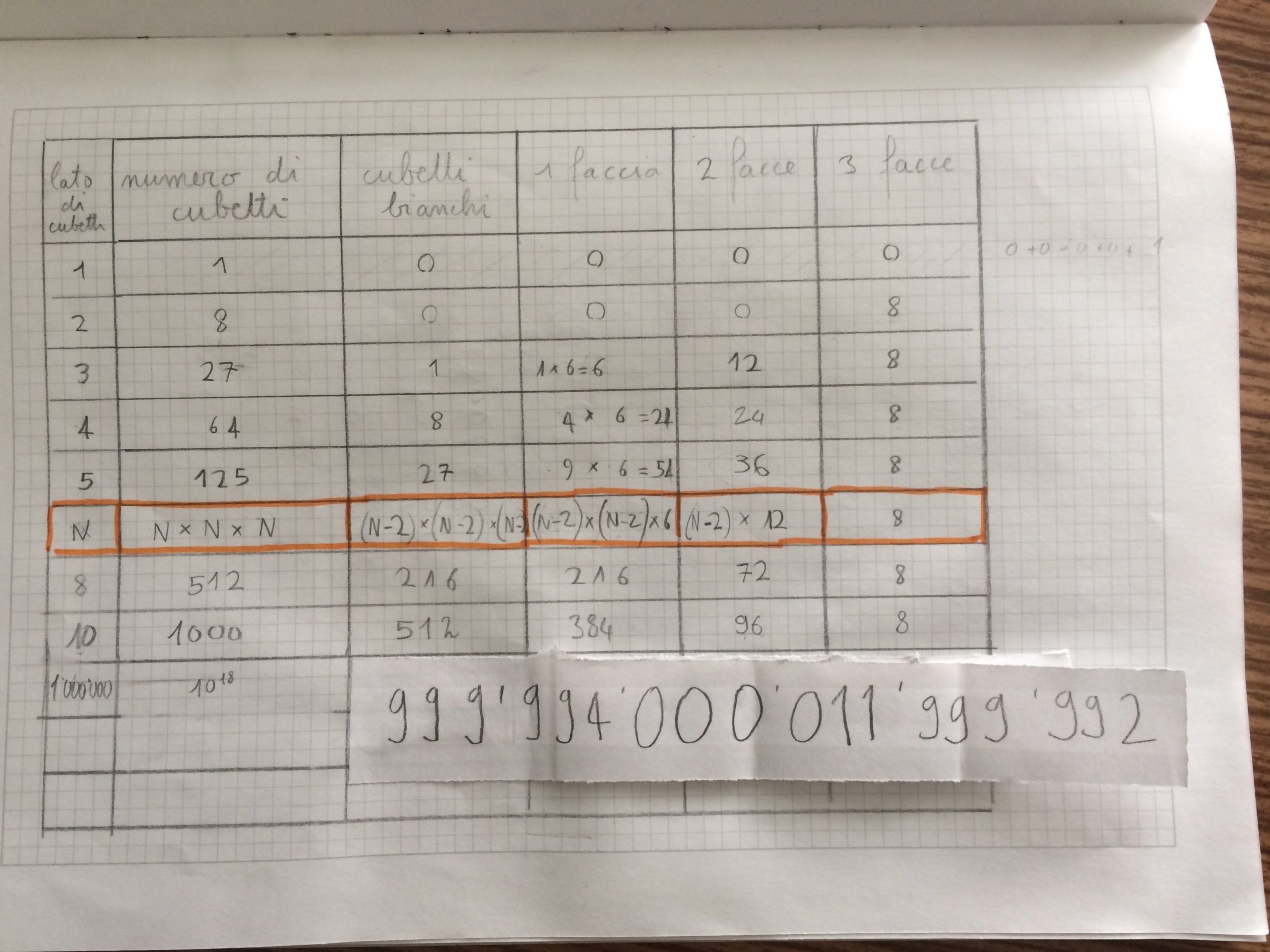
Regole e spiegazioni della tabella:
N = cubetti per lato
x 6= moltiplicare per il numero delle facce del cubo
x 12 = moltiplicare per il numero dei bordi del cubo
8 = numero dei vertici
SECONDA PARTE
Problema 5.
- A) Trova i risultati per un cubo di 1’000’000 di cubetti di alto.
FORMULA
N3
1’ooo’ooo x 1’ooo’ooo x 1’ooo’ooo = 1’ooo’ooo’ooo’ooo’ooo’ooo’ = 1018
- B) Quanti sono i cubetti non pitturati?
FORMULA = (N-2)3
1) esecuzione del calcolo N x N scritto in colonna
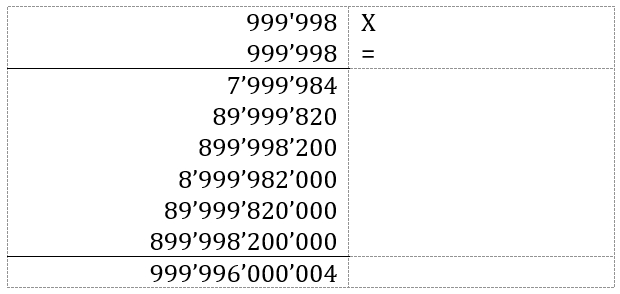
2) lettura del numero: 999 miliardi
996 milioni
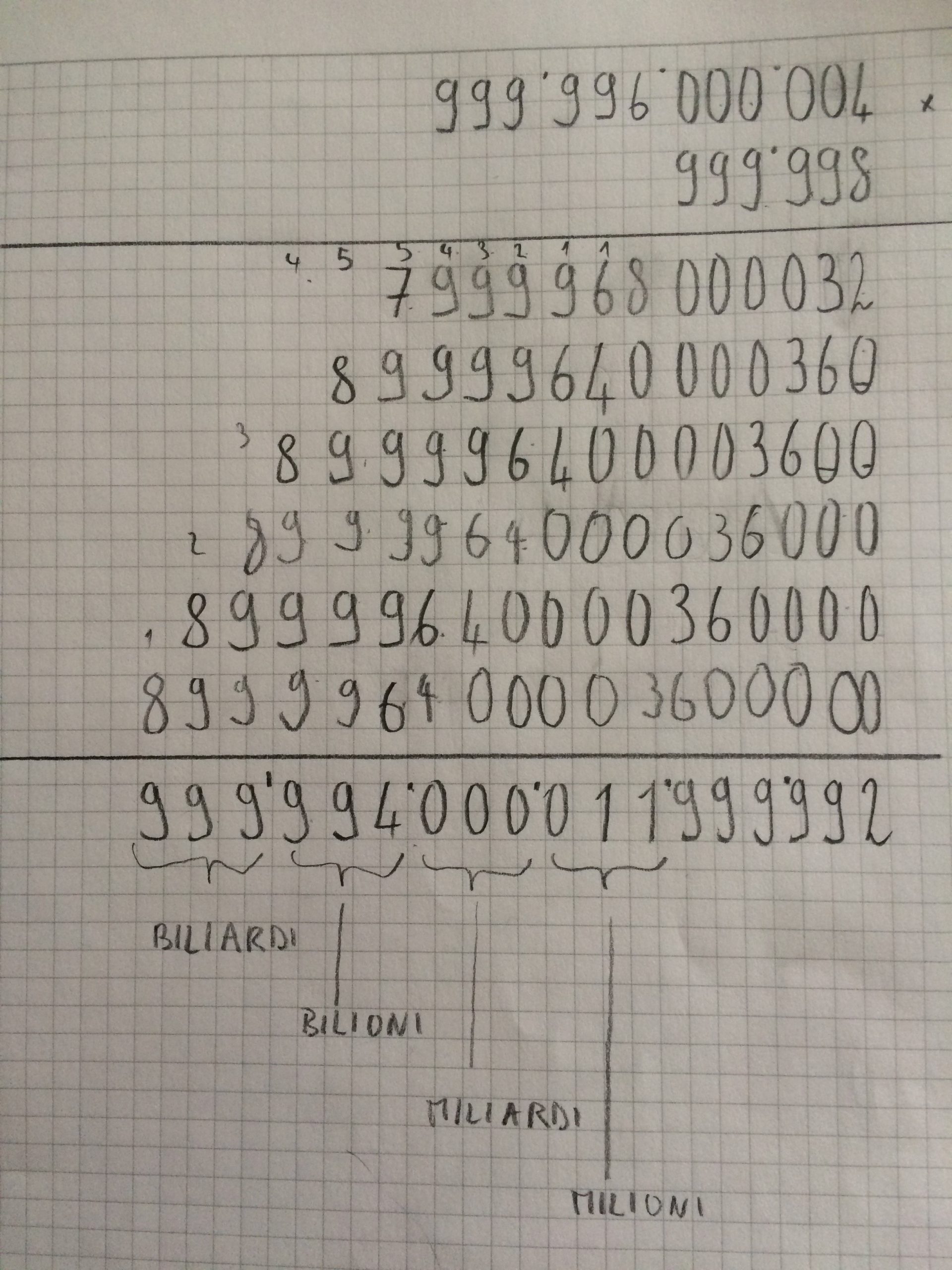
3) esecuzione del calcolo N x N x N scritto in colonna
| 999’996’000’004
999’998 |
X
= |
| 7‘999‘968‘000’032
89’999’640’000’360 899’996’400’003’600 8999’964’000’036’000 89’999’640’000’360’000 899’996’400’003’600’000 |
|
| 999‘994‘000‘011‘999‘992 |
esecuzione e nomenclatura:
Il sitema numerico internzionale
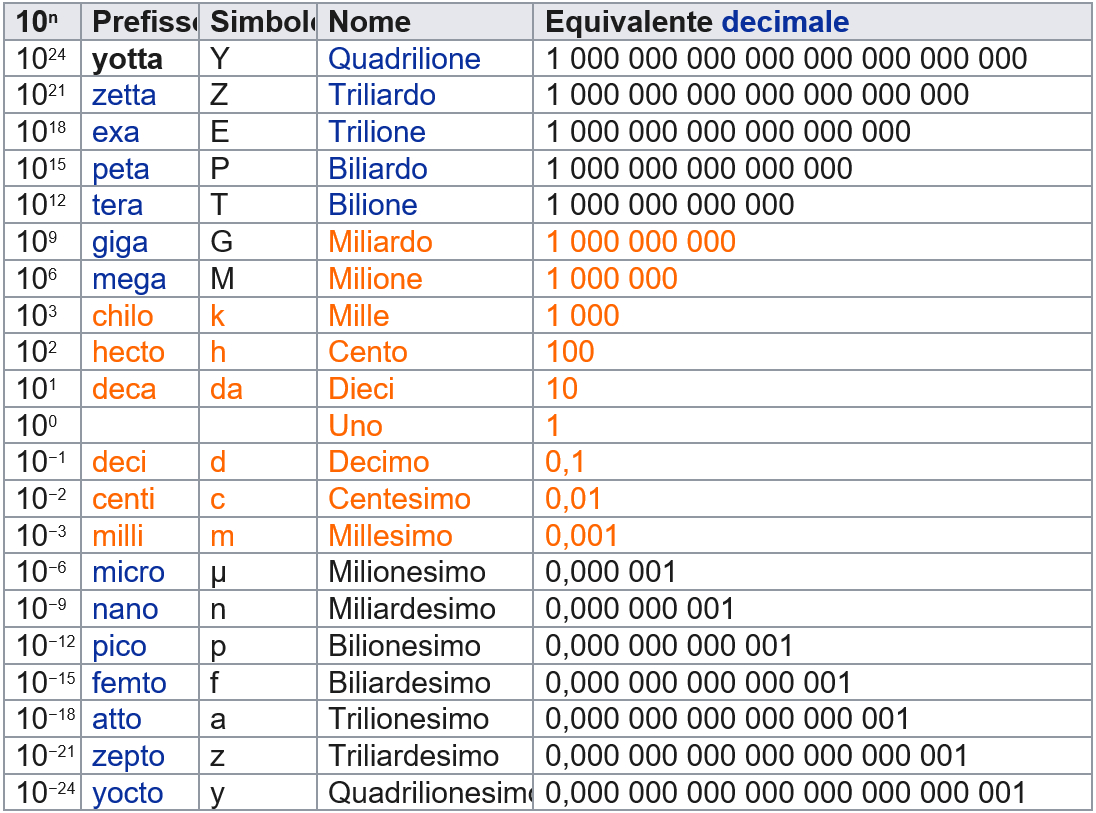
I numeri, scrittura, simboli e nomenclatura dei numeri trattati a scuola.
ALTRI NUMERI
Fantastiliardo https://it.wikipedia.org/wiki/Fantastiliardo
Fatastilione https://it.wikipedia.org/wiki/Fantastilione
Googol https://it.wikipedia.org/wiki/Googol
Yocto https://it.wikipedia.org/wiki/Yocto
